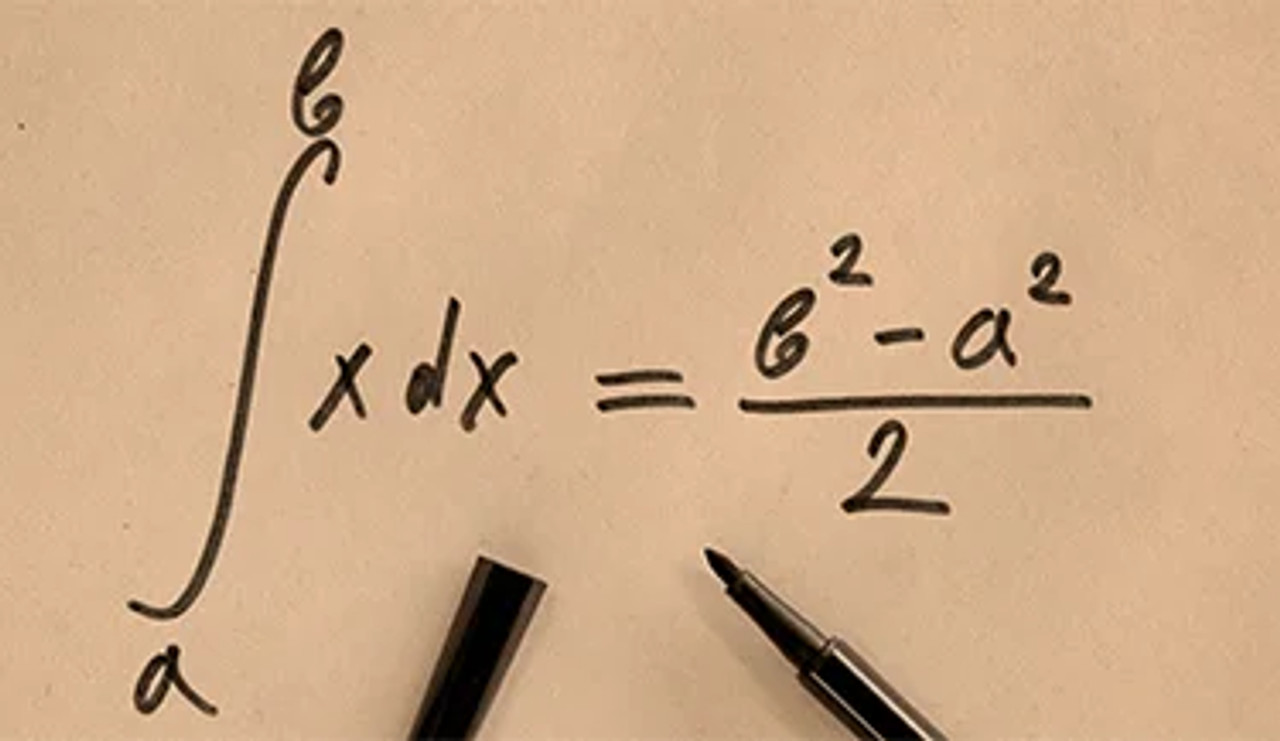
Calculus II

Further expand your understanding of the principles of calculus, like the techniques of integration and logistic models. After completing the course, you will be able to solve integration problems using different techniques of integration.

What you’ll learn

  • Students can complete in as little as 30 days.
  • Mathematics courses have transferred over 10,600 times.
  • 95% of students pass in their first try.
  • Over $600,000 saved in tuition costs.
Calculus II

$79

Plus membership

3 Credits

All courses include:

eTextbooks

2 to 3-day turnaround for grading

Multiple chances to improve your grade

On-demand tutoring & writing center

Student support 7 days a week

$79

Plus membership

3 Credits

All courses include:

eTextbooks

2 to 3-day turnaround for grading

Multiple chances to improve your grade

On-demand tutoring & writing center

Student support 7 days a week

Calculus II

$79

Plus membership

3 Credits

About This Course

|
ACE Approved 2024

Expand on what you learned in General Calculus I with our online General Calculus II course, which covers the techniques of integration, application of integration, exponential and logistic models, parametric equations and polar coordinates, sequence and series, and vector and geometry.

download syllabus

What You'll Learn

Solve integration problems using different techniques of integration: integration table, u-substitution, trigonometric functions, partial fraction, trigonometric substitution, and trapezoidal rule.

Apply integral calculus to compute average value of function, volumes, arc lengths, surface of revolution, and work; as well as moments and centers of mass.

Use various tests to determine the convergence and divergence of sequences and series.

Apply Taylor and Maclaurin series for polynomial approximations.

Demonstrate convergence and divergence of power series.

Solve homogeneous differential equations.

Use differential equations to solve ‘Growth and Decay’ problems.

Sketch parametric and polar curves.

Apply differentiation and integration to parametric equations and polar functions.

Apply dot product and cross product to vectors in R2 and R3.

Apply differentiation to vector functions.

Read Less

lollipops-top-left
lollipops-top-right

Your Life, Your Schedule, Your Education

Transfer into over 3000+ institutions that accept ACE courses or transfer directly into 180+ partner schools.

request information

Course Details

MAT251

|

General Calculus II

This course is designed to further acquaint students with the principles of Calculus. This includes techniques of integration; application of integration; exponential and logistic models; parametric equations and polar coordinates; sequence and series; and vector and geometry.

Prerequisites

Calculus I is a required prerequisite for this course. If you enroll, the assumption is made that you have previously completed Calculus I for credit with a passing score.

Topic Subtopics
An Introduction to Calculus II
  • Welcome to Calculus II
  • Review: Calculus I in 20 minutes
Techniques of Integration
  • An Introduction to the Integral Table
  • Making u-Substitutions
  • An Introduction to Integrals with Powers of Sine and Cosine
  • Integrals with Powers of Sine and Cosine
  • Integrals with Even and Odd Powers of Sine and Cosine
  • Integrals of Other Trigonometric Functions
  • Integrals of Odd Powers of Tangent and Any Power of Secant
  • Integrals with Even Powers of Secant and Any Power of Tangent
  • Repeated Linear Factors: Part One
  • Repeated Linear Factors: Part Two
  • Distinct and Repeated Quadratic Factors
  • Partial Fractions of Transcendental Functions
  • Converting Radicals into Trigonometric Expressions
  • Using Trigonometric Substitution to Integrate Radicals
  • Trigonometric Substitutions on Rational Powers
  • An Overview of Trigonometric Substitution Strategy
  • Trigonometric Substitution Involving a Definite Integral: Part One
  • Trigonometric Substitution Involving a Definite Integral: Part Two
  • Deriving the Trapezoidal Rule
  • An Example of the Trapezoidal Rule
Applications of Integral Calculus
  • Finding the Average Value of a Function
  • Finding the Volumes Using CrossSectional Slices
  • An Example of Finding Cross-Sectional Volumes
  • Solids of Revolution
  • The Disk Method along the y-Axis
  • A Transcendental Example of the Disk Method
  • The Washer Method across the x-Axis
  • The Washer Method across the y-Axis
  • Introducing the Shell Method
  • Why Shells Can Be Better Than Washers
  • The Shell Method: Integrating with Respect to y
  • An Introduction to Arc Length
  • Finding Arc Lengths of Curves Given by Functions
  • Finding Area of a Surface of Revolution
  • An Introduction to Work
  • Calculating Work
  • Hooke’s Law
  • Center of Mass
  • The Center of Mass of a Thin Plate
Sequences and Series
  • The Limit of a Sequence
  • Determining the Limit of a Sequence
  • Monotonic and Bounded Sequences
  • An Introduction to Infinite Series
  • The Summation of Infinite Series
  • Geometric Series
  • Telescoping Series
  • Properties of Convergent Series
  • The nth-Term Test for Divergence
  • An Introduction to the Integral Test
  • Examples of the Integral Test
  • Using the Integral Test
  • Defining p-Series
  • An Introduction to the Direct Comparison Test
  • Using the Direct Comparison Test
  • An Introduction to the Limit Comparison Test
  • Using the Limit Comparison Test
  • Inverting the Series in the Limit Comparison Test
Sequences and Series (continued)
  • Alternating Series
  • The Alternating Series Test
  • Estimating the Sum of an Alternating Series
  • Absolute and Conditional Convergence
  • The Ratio Test
  • Examples of the Ratio Test
  • The Root Test
  • Polynomial Approximations of Elementary Functions
  • Higher-Degree Approximations
  • Taylor Polynomials
  • Maclaurin Polynomials
  • The Remainder of a Taylor Polynomial
  • Approximating the Value of a Function Taylor Series
  • Examples of the Taylor and Maclaurin Series
  • New Taylor Series
  • The Convergence of Taylor Series
  • The Definition of Power Series
  • The Interval and Radius of Convergence
  • Finding the Interval and Radius of Convergence: Part One
  • Finding the Interval and Radius of Convergence: Part Two
  • Finding the Interval and Radius of Convergence: Part Three
  • Differentiation and Integration of Power Series
  • Finding Power Series Representations by Differentiation
  • Finding Power Series Representations by Integration
  • Integrating Functions Using Power Series
Improper Integrals
  • The First Type of Improper Integral
  • The Second Type of Improper Integral
  • Infinite Limits of Integration, Convergence, and Divergence
Differential Equations
  • Solving Separable Differential Equations
  • Finding a Particular Solution
  • Direction Fields
  • Euler's Method for Solving Differential Equations
  • First-Order Linear Differential Equations
  • Separating Homogenous Differential Equations
  • Change of Variables
  • Exponential Growth
  • Logistic Growth
  • Radioactive Decay
Parametric Equations and Polar Coordinates
  • An Introduction to Parametric Equations
  • The Cycloid
  • Eliminating Parameters
  • Derivatives of Parametric Equations
  • Graphing the Elliptic Curve
  • The Arc Length of a Parameterized Curve
  • Finding Arc Lengths of Curves Given by Parametric Equations
  • The Polar Coordinate System
  • Converting between Polar and Cartesian Forms
  • Spirals and Circles
  • Graphing Some Special Polar Functions
  • Calculus and the Rose Curve
  • Finding the Slopes of Tangent Lines in Polar Form
  • Heading toward the Area of a Polar Region
  • Finding the Area of a Polar Region: Part One
  • Finding the Area of a Polar Region: Part Two
  • The Area of a Region bounded by Two Polar Curves: Part One
  • The Area of a Region bounded by Two Polar Curves: Part Two
Vectors and the Geometry of R² and R³
  • Coordinate Geometry in Three Dimensional Space
  • Introduction to Vectors
  • Vectors in R² and R³
  • An Introduction to the Dot Product
  • Orthogonal Projections
  • An Introduction to the Cross Product
  • Geometry of the Cross Product
  • Equations of Lines and Planes in R³
  • Introduction to Vector Functions
  • Derivatives of Vector Functions
  • Vector Functions: Smooth Curves
  • Vector Functions: Velocity and Acceleration

Your score provides a percentage score and letter grade for each course. A passing percentage is 70% or higher.

Assignments for this course include:

  • 3 Graded Topic Reviews
  • 3 Graded Quizzes
  • 3 Graded Exams
  • 1 Graded Final

This course does not require a text.


Student Success students also take:

Microbiology

Microbiology Lab

Microeconomics


Helpful resources:

Why AP Calculus is the Scariest AP Test of All

Do You Have to Take Math in College?

Tips to Help College Students to Succeed in an Online Math Course

It was time for my next big thing.

Straighterline made it very easy and convenient to take all the prerequisites I needed to take to advance my career in Science. I liked how flexible it was. I would highly recommend it to anyone.

Things I love about StraighterLine

Time for me

I was able to fit classes into my free time and spend 10 hours a week when I was available.

Variety of courses

I took five courses with StraighterLine and saved thousands of dollars on my degree.

!

Added To Cart

Your cart includes: